

The above problem (and all inclined plane problems) can be simplified through a useful trick known as "tilting the head." An inclined plane problem is in every way like any other net force problem with the sole exception that the surface has been tilted. The net force is 5 N, directed along the incline towards the floor. The parallel component and the friction force add together to yield 5 N. The perpendicular component and the normal force add to 0 N. That is, all the individual forces are added together as vectors. As in all net force problems, the net force is the vector sum of all the forces. Yet the frictional force must also be considered when determining the net force. The perpendicular component of force still balances the normal force since objects do not accelerate perpendicular to the incline. In the presence of friction or other forces (applied force, tensional forces, etc.), the situation is slightly more complicated. (in the absence of friction and other forces) In the absence of friction and other forces (tension, applied, etc.), the acceleration of an object on an incline is the value of the parallel component (m*g*sine of angle) divided by the mass (m).
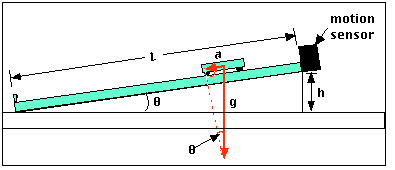
The equations for the parallel and perpendicular components are: The task of determining the magnitude of the two components of the force of gravity is a mere manner of using the equations. The parallel component of the force of gravity is the net force. It is the parallel component of the force of gravity that causes this acceleration. This object will subsequently accelerate down the inclined plane due to the presence of an unbalanced force. The parallel component of the force of gravity is not balanced by any other force. The perpendicular component of the force of gravity is directed opposite the normal force and as such balances the normal force. The diagram below shows how the force of gravity has been replaced by two components - a parallel and a perpendicular component of force. The force of gravity will be resolved into two components of force - one directed parallel to the inclined surface and the other directed perpendicular to the inclined surface. This is the second peculiarity of inclined plane problems. Instead, the process of analyzing the forces acting upon objects on inclined planes will involve resolving the weight vector (F grav) into two perpendicular components. However, this is not the process that we will pursue with inclined planes. Usually, any force directed at an angle to the horizontal is resolved into horizontal and vertical components. Thus, one (or more) of the forces will have to be resolved into perpendicular components so that they can be easily added to the other forces acting upon the object. The task of determining the net force acting upon an object on an inclined plane is a difficult manner since the two (or more) forces are not directed in opposite directions. The truth about normal forces is not that they are always upwards, but rather that they are always directed perpendicular to the surface that the object is on. But this is only because the objects were always on horizontal surfaces and never upon inclined planes. Up to this point in the course, we have always seen normal forces acting in an upward direction, opposite the direction of the force of gravity. The first peculiarity of inclined plane problems is that the normal force is not directed in the direction that we are accustomed to. The force of gravity (also known as weight) acts in a downward direction yet the normal force acts in a direction perpendicular to the surface (in fact, normal means "perpendicular"). As shown in the diagram, there are always at least two forces acting upon any object that is positioned on an inclined plane - the force of gravity and the normal force. The diagram at the right depicts the two forces acting upon a crate that is positioned on an inclined plane (assumed to be friction-free). To understand this type of motion, it is important to analyze the forces acting upon an object on an inclined plane. Objects are known to accelerate down inclined planes because of an unbalanced force. In physics, a tilted surface is called an inclined plane. The rate at which the object slides down the surface is dependent upon how tilted the surface is the greater the tilt of the surface, the faster the rate at which the object will slide down it. An object placed on a tilted surface will often slide down the surface.


 0 kommentar(er)
0 kommentar(er)
